Коды с повторением и инверсией

К другим кодам, позволяющим обеспечить минимальное кодовое расстояние d_min = 3 или d_min = 4, могут быть отнесены двоичные коды с повторением и инверсией. Они строятся по следующему принципу:

• записываются все кодовые комбинации неизбыточного кода M = 2^m;
• к каждой кодовой комбинации добавляется точно такая же, если исходная комбинация содержала четное число единиц, или инверсная, если исходная комбинация содержала нечетное число единиц.

Можно показать, что такие коды позволяют получить минимальное кодовое расстояние d_min = m при m ≤ 4 и d_min = 4 при d_min > 4.

Пример

Построить код с повторением и инверсией, если m = 3, M = 2^m = 8.

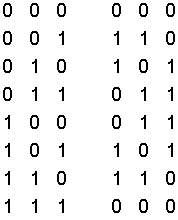
Легко видно, d_min = 3, а избыточность кода

.

Пример

Построить код с повторением и инверсией, если m = 4, M = 2^m = 16.

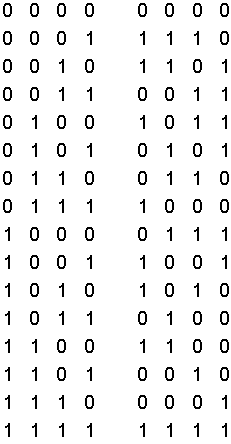
Для этого кода d_min = 4, то есть он способен обнаружить три ошибки в режиме обнаружения и исправить одну ошибку в режиме исправления. При отыскании ближайшей кодовой комбинации применим метод максимального правдоподобия, а также некоторые алгоритмы.