Двоичные коды с минимальным кодовым расстоянием dmin= 3
Коды с dmin = 3 являются первыми корректирующими кодами, разработанными в рамках теории кодирования. Они способны исправлять одну ошибку. Коды, разработанные Хеммингом до сих пор широко применяются и считаются одними из лучших.
Рассмотрим построение двоичного кода Хемминга с dmin = 3.
Постановка задачи: для заданного количества рабочих комбинаций M = 2m и заданной величины минимального кодового расстояния dmin = 3:
- определить требуемую избыточность;
- разработать регулярный метод записи кодовых комбинаций.
Ответ на первый вопрос можно найти, применяя формулу (10) для определения минимальной величины k:
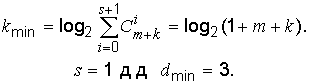
Из этой формулы k определяется методом подбора.
Получим ответ на второй вопрос. Для исправления ошибки надо знать место ее возникновения, или номер позиции в коде, где произошла ошибка. Для определения места ошибки или номера искаженной позиции используется избыточность. Избыточные элементы должны содержать всю необходимую информацию для решения задачи. Количество различных сообщений о номере искаженной позиции равно (n + 1) (единица добавляется для учета отсутствия искажений). Вероятность любого из этих сообщений одинакова. Количество избыточных элементов можно определить из выражения
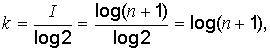
что совпадает с границей, определяемой по формуле Хемминга.
Этот результат можно получить еще одним способом. Будем использовать избыточные элементы так, чтобы можно было однозначно определить место искаженной позиции. Для этого предлагается проводить k проверок четности суммы единиц, стоящих на определенных позициях. В результате каждой проверки будем записывать “0”, если четность подтверждается значением избыточного элемента, или “1”, если число единиц нечетно. Далее запишем все результаты проверок на четность последовательно друг за другом: E1, E2,…, Ei,…, Ek. В результате получим некоторое двоичное k-разрядное число, которое называется проверочным (контрольным). Потребуем, чтобы это число указывало номер искаженной позиции. То есть для каждого E должно найтись свое число 2k = n + 1.
В процессе проверок должны учитываться следующие позиции:
1-я проверка – позиции 1, 3, 5, 7,…;
2-я проверка – позиции 2, 3, 6, 7, 10,…;
3я проверка – позиции 4, 5, 6, 7, 12, 14…;
4-я проверка – позиции 8, 9, 11, 12, 13…;
…
i-я проверка – позиции 2i-1,
2i-1 + 1,…;
…
k-я проверка – позиции 2k-1,
2k-1 + 1,…;
Пример
Построить код Хемминга для восьми комбинаций (M = 8) с минимальным кодовым расстоянием dmin = 3.
![]()
Код приведен в табл. 3.
Табл. 3
| Состояние позиций кода | № кодовой комбинации | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 2 |
| 1 | 0 | 0 | 1 | 1 | 0 | 3 |
| 1 | 1 | 0 | 0 | 1 | 1 | 4 |
| 1 | 1 | 1 | 0 | 0 | 0 | 5 |
| 1 | 0 | 1 | 1 | 0 | 1 | 6 |
| 0 | 1 | 1 | 1 | 1 | 0 | 7 |
| 0 | 0 | 1 | 0 | 1 | 1 | 8 |
Элементы в позиции №1 получаются при суммировании по модулю два элементов в позициях №3 и №5, в позиции №2 – суммированием элементов в позициях №3 и №6, в позиции №4 – суммированием элементов в позициях №5 и №6.
Для построения кода с минимальным кодовым расстоянием dmin = 4 по тем же исходным данным можно воспользоваться следующей теоремой кодирования: для достижения четного минимального кодового расстояния к коду с нечетным минимальным кодовым расстоянием, на единицу меньшим исходного, добавляют еще один бит проверки на четность. Таким образом, получаем код, приведенный в табл. 4.
Табл. 4
| Состояние позиций кода | № кодовой комбинации | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 2 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 3 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 4 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 5 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 7 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 8 |