Двоичные итеративные коды

Двоичные итеративные коды строятся по следующим правилам.

Записываются всевозможные комбинации двоичного неизбыточного кода. Их число M = 2^m. Каждая кодовая комбинация разбивается на отрезков по m₀ элементов в каждом так, чтобы выполнялось условие .

Если это условие имеет вид неравенства, то последний отрезок может быть дополнен

нулями. Полученные отрезки располагаются в виде матрицы:

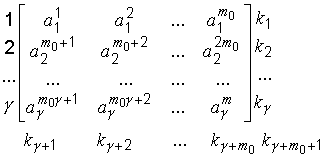
Каждая строка матрицы проверяется на четность и дополняется проверочным элементом

Аналогичным образом проверяются на четность все столбцы матрицы, и формируются элементы

Формируется элемент

,

который проверяет на четность строку или столбец из проверочных символов.

В итоге каждая строка матрицы будет представлять собой код с минимальным кодовым расстоянием d_minСТР = 2, и каждый столбец тоже будет являться комбинацией кода с d_{minСТОЛБ} = 2. В целом же код обеспечивает минимальное кодовое расстояние d_min = d_minСТР

.

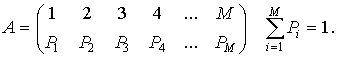В общем случае проверки по строкам и по столбцам могут быть организованы и по более сложной логике (необязательно одинаковой для столбцов и строк). Например, строки можно проверить по логике кода с повторением и инверсией и получить минимальное кодовое расстояние величиной до четырех, а столбцы можно проверить по логике кода с проверкой на четность и получить минимальное кодовое расстояние по столбцам, равное двум. Итоговое же d_min = d_minСТР* d_{minСТОЛБ} = 2 * 4 = 8.

Пример. Допустим, имеется неизбыточный двоичный код с параметрами i = 2⁹ и m = 9. Разобьем кодовую комбинацию на три отрезка по три элемента в каждом ( = 3 m₀ = 3). В данном случае выполняется равенство

Рассмотрим некоторую кодовую комбинацию, например, a_i= 100111011. Составим для нее матрицу, используя правила, приведенные выше.

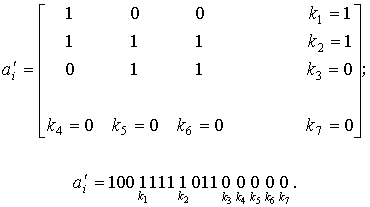
Комбинация a’_i имеет результирующее минимальное кодовое расстояние d_min = 4. Она передается в канал связи строка за строкой.

После приема комбинации a’_i она снова представляется в виде матрицы.

Если код используется только в режиме обнаружения ошибок, он может обнаружить любую ошибку кратности от 1 до 3 по нарушению четности в строке или столбце. Если код используется в режиме исправления ошибок, он может исправить любую одиночную ошибку (s = 1). При этом ошибочный символ будет находиться на пересечении той строки и того столбца, в которых обнаружены нарушения четности.

Пусть принята искаженная комбинация b_i, матричное представление которой имеет вид:

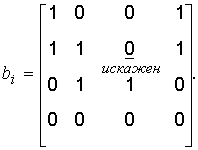
После проведения проверок устанавливается позиция ошибки.

---