Пропускная способность систем передачи информации

Одной из основных характеристик любой системы передачи информации, кроме перечисленных выше, является ее пропускная способность.

Пропускная способность – максимально возможное количество полезной информации, передаваемое в единицу времени:

c = max{I_max} / T_C ,

c = [бит/с].

Иногда скорость передачи информации определяют как максимальное количество полезной информации в одно элементарном сигнале:

s = max{I_max} / n,,

s = [бит/элемент].

Рассмотренные характеристики зависят только от канала связи и его характеристик и не зависят от источника.

Пропускная способность дискретного канала связи без помех. В канале связи без помех информацию можно передавать неизбыточным сигналом. При этом число n = m, а энтропия элементарного сигнала H_Cmax = logK.

max{I_C} = nH_Cmax= mH_Cmax .

Длительность элементарного сигнала , где – длительность элементарного сигнала.

где F_C – спектр сигнала.

Пропускная способность канала связи без помех

Введем понятие скорости генерации элементарного сигнала источником информации:

Тогда, используя новое понятие, можно преобразовать формулу для скорости передачи информации:

c = BlogK.

Полученная формула определяет максимально возможную скорость передачи информации в дискретном канале связи без помех. Это следует из предположения о том, что энтропия сигнала максимальна.

Если H_C < H_Cmax, то c = BH_C и не является максимально возможной для данного канала связи.

Пропускная способность дискретного канала связи с помехами. В дискретном канале связи с помехами наблюдается ситуация, изображенная на рис. 6.

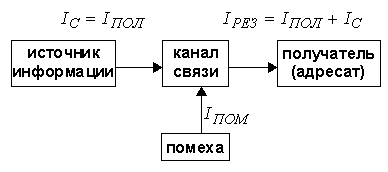
Рис.6

Учитывая свойство аддитивности, а также формулы Шеннона для определения количества информации, рассмотренные выше, можно записать

I_C = T_C F_C log(A_K P_C),

I_ПОМ = T_П F_П log(AP_П).

Для получателя источник полезной информации и источник помехи равноценны, поэтому нельзя на приемной стороне выделить составляющую помехи в сигнале с результирующей информацией

I_РЕЗ = T_C F_C log(A_K (P_П + P_C)), если T_C = T_П , F_C = F_{П .}

Приемник может быть узкополосным, а помеха находиться в других интервалах частот. В этом случае она не будет влиять на сигнал.

Будем определять результирующий сигнал для наиболее “неприятного” случая, когда параметры сигнала и помехи близки друг к другу или совпадают. Полезная информация определяется выражением

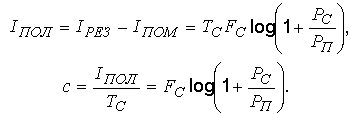
Эта формула получена Шенноном. Она определяет скорость передачи информации по каналу связи в случае, если сигнал имеет мощность P_C, а помеха – мощность P_П. Все сообщения при такой скорости передадутся с абсолютной достоверностью.

Формула не содержит ответа на вопрос о способе достижения такой скорости, но дает максимально возможное значение с в канале связи с помехами, то есть такое значение скорости передачи, при которой полученная информация будет абсолютно достоверной.

На практике экономичнее допустить определенную долю ошибочности сообщения, хотя скорость передачи при этом увеличится.

Рассмотрим случай P_C >> P_П. Если ввести понятие отношения сигнал/шум

P_C >> P_П означает, что . Тогда

Полученная формула отражает предельную скорость мощного сигнала в канале связи.

Если P_C << P_П , то с стремится к нулю. То есть сигнал принимается на фоне помех. В таком канале в единицу времени сигнал получить не удается.

В реальных ситуациях полностью помеху отфильтровать нельзя. Поэтому приемник получает полезную информацию с некоторым набором ошибочных символов. Канал связи для такой ситуации можно представить в виде, изображенном на рис. 7, приняв источник информации за множество передаваемых символов {X}, а приемник – за множество получаемых символов {Y}.

Рис.7 Граф переходных вероятностей K- ичного канала связи

Между существует определенное однозначное соответствие. Если помех нет, то вероятность однозначного соответствия равна единице, в противном случае она меньше единицы.

Если q_i – вероятность принятия y_i за x_i, a p_ij = p{y_i / x_i} – вероятность ошибки, то

.

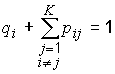Граф переходных вероятностей отражает конечный результат влияния помехи на сигнал. Как правило, он получается экспериментально.

Полезная информация может быть оценена как I_ПОЛ = nH(X · Y), где n – количество элементарных символов в сигнале; H(X · Y) – взаимная энтропия источника X и источника Y.

В данном случае источником X является источник полезной информации, а источником Y является приемник. Соотношение, определяющее полезную информацию, можно получить исходя из смысла взаимной энтропии: заштрихованный участок диаграммы определяет сообщения, переданные источником X и полученные приемником Y; незаштрихованные участки отображают сигналы источника X, не дошедшие до приемника и полученные приемником посторонние сигналы, не передаваемые источником.

B – скорость генерации элементарных символов на выходе источника.

Для получения max[H(Y) – H(Y/X)] нужно по возможности увеличить H(Y) и уменьшить H(Y/X). Графически эта ситуация может быть представлена совмещением кругов на диаграмме (Рис. 2г).

Если же круги вообще не пересекаются, X и Y существуют независимо друг от друга.

В дальнейшем будет показано, как можно использовать общее выражение для максимальной скорости передачи при анализе конкретных каналов связи.

---