Связь между количеством информации в сигнале

Интуитивно можно сделать предположение о связи между количеством информации в сигнале и его объемом: чем больше сигнал, тем больше информации он может переносить.

Пусть параметры передаваемого сигнала: n – число элементарных символов, K – основание кода. Тогда I_max = nlogK. С другой стороны

.

Если длительность сигнала , то . По теореме Котельникова, спектр одиночного импульса , то есть чем короче импульс, тем большим спектром он обладает. Два сомножителя в формулах

совпадают.

Если под K понимать амплитудные градации, в отсутствии помех ( – порог чувствительности). Это соотношение адекватно описывает ситуацию, если уровень помех не превышает величины .

В канале связи с помехами

.

То есть между величинами K и (P_C / P_П) существует связь. В выражении (P_C / P_П) скрыта информация о плотности.

Можно доказать, что количество информации в сигнале может быть определено как

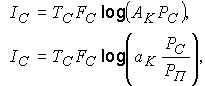
где A_K = const, a_K = const зависят от характеристик помех в канале связи и от способов выбора расстояния между отдельными градациями сигнала. Зная a_K, можно рационально распоряжаться сигналом. Перепишем последнюю формулу в ином виде:

В этой формуле слагаемое V_C определяет полезную информацию, переносимую сигналом, а слагаемое T_C F_C log(a_K) – дополнительную информацию, отражающую плотность упаковки сигнала и способов выделения отдельных градаций, то есть способов получения K, это дополнительная информация.

Иногда пользуются понятием удельной содержательности сигнала

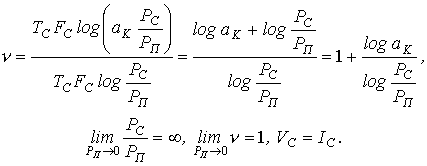
Рассмотренный предельный случай свидетельствует о том, что в канале связи без помех можно не передавать дополнительной информации.