Связанные источники сообщений (объединения)

До сих пор предполагалось, что источник сообщения единственен. Однако существует ситуация, когда информация к получателю поступает от двух или более источников одновременно. В таких случаях говорят, что источники называются связанными и называют их объединениями. Степень связанности источников оценивается вероятностями появления сообщений одновременно от нескольких источников.

Пусть первый источник характеризуется ансамблем

Второй источник представлен другим ансамблем

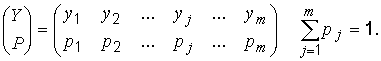
Степень связанности источников можно охарактеризовать следующей матрицей:

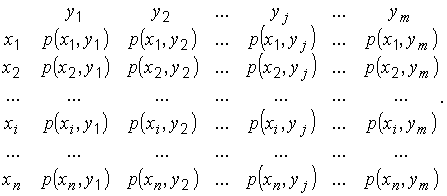
Вероятность одновременного появления сообщений x_i и y_j обозначена p(x_i, y_j). Если появилось сообщение от одного источника, то с определенной вероятностью поступит сообщение от другого источника, если соответствующий элемент в матрице связей ненулевой. Чем большее число вероятностей в матрице отлично от нуля, тем больше связь между источниками.

Если в этой матрице все вероятности p_ij = 0, то источники не являются коррелированными, и сообщения передаются независимо друг от друга. Однако наиболее вероятна ситуация существования связи между источниками. Одним из источников может быть помеха.

Если источников больше двух, можно построить матрицу для двух источников, которую затем рассматривать как эквивалентный источник.

Введем энтропийные характеристики для объединения. Пусть p(x_i) – априорная вероятность появления сообщения x_i.

Можно говорить об энтропии источника X:

.

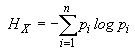Аналогично для источника Y априорная вероятность появления сообщения p(y_j) и энтропия

.

Если p(x_i, y_j) – вероятность совместного появления сообщений от источников X, Y, то

.

Введем другие характеристики. Условная энтропия определяется следующим образом:

Взаимная энтропия

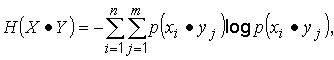
где p(x_i, · y_j) – взаимная вероятность, которая характеризует обязательное появление сообщений от двух источников одновременно; фактически p(x_i, · y_j) является частным случаем вероятности p(x_i,, y_j).

Можно установить графически (Табл. 2) или аналитически связь между любой парой введенных энтропийных характеристик.

Табл. 2 Графическая связь между энтропийными характеристиками

Наименование	Обозначение	Соотношение	Иллюстративная диаграмма
Безусловная (априорная) энтропия			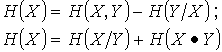Рис. 2а)
Условная энтропия			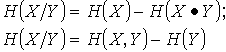Рис. 2б)
Совместная энтропия			Рис. 2в)
Взаимная энтропия			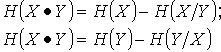Рис. 2г)

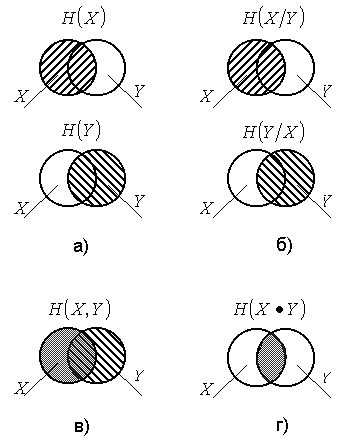
Рис. 2 Энтропийные характеристики

Связь между различными энтропиями может быть получена аналитически. Выразим, например, H(X,Y) через другие энтропийные характеристики.

Известно, что

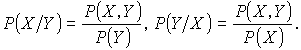
Предварительно установим связь между совместной, условной и безусловной вероятностями:

Таким образом, формула H(X/Y) = H(X,Y) – H(Y) была получена аналитически.

Относительно энтропийных характеристик можно также сказать, что выполняется соотношение H(X) < H(X/Y). H(X/Y) – среднее количество информации, полученное от источника X при условии, что уже получено сообщение от Y. H(X) – среднее количество информации, полученное от источника X независимо от того, получено ли сообщение от другого источника.

Чаще адресат находится на большом расстоянии от источника. Задача передачи информации в теории информации является основной. Для ее решения необходимо определить количество информации. Условием оптимальной передачи информации является равновероятность сообщений, то есть максимальная энтропия. а значит и максимальное количество информации.

---