Понятие о минимальном кодовом расстоянии

Одним из основных понятий, на котором базируется любая теория помехоустойчивого кодирования, является понятие о кодовом расстоянии вообще и о минимальном кодовом расстоянии в частности.

Пример. Допустим, m = 8, и сообщения закодированы простым неизбыточным двоичным кодом. Тогда из выражения M = 2ⁿ = 2^m следует m = n = 3. Список рабочих комбинаций имеет следующий вид:

Изобразим так называемую геометрическую модель кода, вводя систему координат из трех осей, каждая из которых отображает один из разрядов. Модель кода – куб (рис.25). Каждая кодовая комбинация отображается одной из вершин куба. Будем называть ребро кубы, определяющее две соседние кодовые комбинации, одним кодовым переходом и рассматривать как единичное расстояние между двумя соседними кодовыми комбинациями. Кодовым расстоянием между парой любых кодовых комбинаций будем называть минимальное число ребер (кодовых переходов), разделяющих эти комбинации:

кодовых переходов .

Например,

Рис. 25 Геометрическая модель двоичного трехразрядного кода

Понятие минимального кодового расстояния характеризует код в целом. Минимальным кодовым расстоянием d_min является минимум среди всех кодовых расстояний данного кода, то есть определяется по всем возможным парам кодовых комбинаций данного кода

Для рассматриваемого кода d_min= 1. Учитывая, что рассматриваемый код по построению является неизбыточным, можно утверждать, что любой неизбыточный код имеет d_min= 1 и наоборот, если d_min= 1, код является неизбыточным.

Из геометрической модели кода видно, что любая, даже одиночная, ошибка не может быть обнаружена кодом с d_min= 1, так как любая кодовая комбинация, в которой произошла ошибка, переместившись на один кодовый переход, совпадет с соседней кодовой комбинацией и будет разрешенной.

Для построения простейшего избыточного кода, который может обнаруживать одну ошибку (r = 1) нужно отобрать рабочие комбинации на расстоянии

В рассматриваемом коде можно выбрать следующие комбинации:

где M_РАБ – число рабочих комбинаций.

Избыточность полученного кода

.

Если требуется обнаруживать две ошибки (r = 2), то рабочих комбинаций будет только две (например, 000 и 111), минимальное кодовое расстояние в этом случае d_min = 3, избыточность

.

Если r = 3, d_min≥ 4, что невозможно обеспечить в рассматриваемом коде, так как кодовое расстояние

.

Если бы сообщения кодировались неизбыточным кодом, то для получения четырех кодовых комбинаций потребовалось бы m = 2 информационных элементов.

В двоичных кодах кодовое расстояние между любыми двумя комбинациями можно определить как число отличающихся разрядов.

В общем случае в кодах, используемых в режиме обнаружения ошибок кратности r должно обеспечиваться минимальное кодовое расстояние

d_min ≥ r + 1. (4)

Определим минимальное кодовое расстояние в кодах, работающих в режиме исправления s ошибок.

Для исправления s ошибок нужно, очевидно, искаженную кодовую комбинацию b_i отождествить с комбинацией a_i, которая является рабочей и из которой b_i получилась в результате s искажений. Такое отождествление производится на базе критерия правдоподобия, под которым понимается

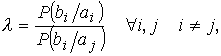
где P(b_i / a_i) – вероятность образования b_i из a_i;

P(a_i / b_i) – вероятность образования a_i из b_i.

λ сравнивается с некоторым пороговым значением, чаще всего с единицей. Если λ > 1, то выносится решение о том, что b_i получилось из a_i. Если λ < 1, то выносится решение о том, что b_i нельзя отождествлять с a_i.

Значения условных вероятностей, необходимых для вычисления λ, нельзя установить непосредственно, но можно воспользоваться связью между ними и соответствующими кодовыми расстояниями. Из факта уменьшения вероятности появления ошибки при увеличении ее кратности следует:

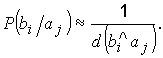
Кодовое расстояние между b_i и a_i равно

.

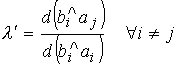Если , то b_i получилось из a_j, так как a_i ближе к b_i, чем a_i. Если , то b_i получилось из a_i.

Геометрически этот результат можно интерпретировать следующим образом:

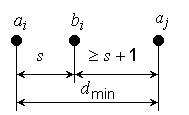
Минимальное расстояние кода, работающего в режиме исправления s ошибок,

d_min ≥ 2s + 1. (5)

По аналогии можно утверждать, что код, способный обнаруживать r ошибок и исправлять s из них, должен иметь минимальное кодовое расстояние

d_min ≥ r + s + 1 (r ≥ s). (6)

Выражения (5) и (6) не противоречат друг другу, так как прежде чем исправлять ошибку, ее надо сначала обнаружить

Можно показать, что для исправления e ошибок стирания нужно обеспечить минимальное кодовое расстояние

d_min ≥ e + 1. (7)

В общем случае для обнаружения r ошибок трансформации, исправления s из них и для исправления e ошибок стирания нужно обеспечить минимальное кодовое расстояние

d_min ≥ r + s + e + 1 (r ≥ s). (8)

Выражения (4) - (7) вытекают из (8).

---