Погрешности, вносимые каналом связи

Будем считать, что значения измеряемой величины (то есть значения ближайших уровней) передаются некоторым n -элементным двоичным кодом с минимальным кодовым расстоянием d_min. Выше отмечалось, что d_min вводится чаще всего для использования кода в режиме обнаружения ошибок. Будем считать, что этот принцип применяется и в КС ТИ.

Значение измеряемой величины может быть принято правильно с некоторой вероятностью Р_ПР = (1 – р₀)ⁿ; в этом случае погрешность, вносимая каналом связи .

Может быть зафиксирован ложный прием с некоторой вероятностью Р_{Л ПР}, зависящей от формата передачи данных. В этом случае возникает погрешность, так как значение уровня N₁ переходит в значение N₂.

Может возникнуть ситуация защитного отказа с вероятностью Р_{З ОТ}. В зависимости от условия наличия обратной связи вероятность ложного приема может быть оценено по-разному.

Если обратная связь отсутствует, то

.

В системах с обратной связью посылается запрос на повторение. Однако любая повторная передача влечет за собой рост величины T₀. За время повтора измеряемая величина продолжает изменяться. Таким образом, в данном случае погрешность возникает за счет запаздывания. Аналогом такой ситуации может быть циклический контроль. Вероятность погрешности зависит от вероятности ложного приема Р_{Л ПР} и от вероятности защитного отказа Р_{З ОТ}.

Рассмотрим погрешность, возникающую при ложном приеме. Допустим, при передаче сообщения, соответствующего i -му уровню, с частотой принимается сообщение, соответствующее j -му уровню. Для простоты в дальнейшем будем обозначать i = N_i = A_i , j = N_j = A_j. Тогда погрешности, вносимые каналом связи можно представить следующим образом:

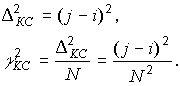
Выражение для нужно дополнить произведением вероятностей передачи i -го уровня и приема вместо него j -го уровня:

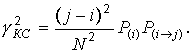
Для получения результирующей погрешности канала связи просуммируем по всем уровням:

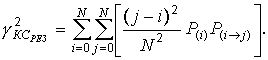
Воспользоваться этой формулой можно в случае, когда известны Р_(i) и P_{(i → j)}. Если заранее ничего неизвестно об измеряемой величине, считают все вероятности передачи уровня одинаковыми: P₍₁₎ = P₍₂₎ = … = P_(N) = 1 / (N + 1). Это предположение может не выполняться, если величина имеет номинальное значение и допускает лишь некоторые отклонения от него. P_{(i → j)} = P_{Л ПР} и не зависит от i и j для большинства кодов. В этом случае

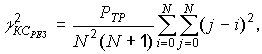
где Р_ТР – вероятность ошибки трансформации.

С учетом того, что

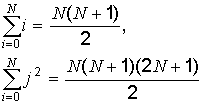
получим

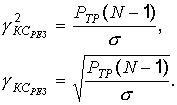
Анализируя полученные формулы погрешностей передатчика и канала связи, можно заметить, что для погрешность передатчика с ростом числа уровней N погрешность уменьшается, а погрешность канала связи увеличивается. Но в выражении погрешности для передатчика под знаком корня находится N², а в выражении для канала связи – N (в этом случае влияние роста N устраняется еще и малой величиной Р_ТР). Поэтому N следует выбирать, используя формулу погрешности передатчика.

При наличии защитного отказа значение измеряемой величины A(t) может быть зафиксировано через интервал времени T₀ с вероятностью (1 – Р_{З ОТ}). Если при этом

,

сообщение было принято ложно, если же , сообщение было принято верно. При повторной передаче интервал времени между съемами информации становится равным 2Т₀, Р_{З ОТ}(1 – Р_{З ОТ}). При i -й передаче сообщение будет принято (ложно или правильно) с вероятностью (Р_{З ОТ})^i-1(1 – Р_{З ОТ}). Среднее значение цикла определяется следующим образом:

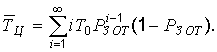
При вероятность .

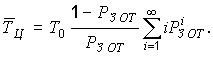
При под знаком суммы имеем неопределенность типа . После раскрытия этой неопределенности получаем

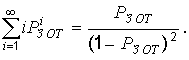
В итоге

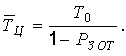
Погрешность может быть оценена опосредованно через передатчик путем подстановки в формулу определения погрешности передатчика вместо T₀ значение T_Ц. Правомерность такого шага можно объяснить тем, что повторное сообщение после запроса проходит через передатчик.

---