Погрешность передающего устройства

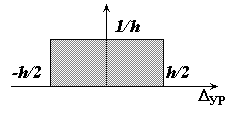
Передающее устройство аналоговый сигнал на входе должно преобразовать в цифровой код (обычно двоичный). Для решения этой задачи необходимо реализовать два принципа квантования: по уровню и по времени.

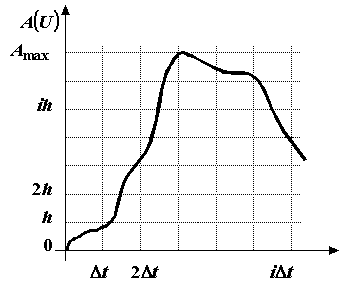
Рис. 20

Преобразование величины в код осуществляется в дискретные моменты времени; при этом в каждый момент времени фиксируется не истинное значение величины, а значение ближайшего уровня. Квантование по уровню применяется для того, чтобы сделать множество фиксируемых значений измеряемой величины конечным, а значит, и использовать конечное число кодов с обеспечением конечного времени передачи. Квантование по времени необходимо, так как код требует определенного времени для передачи. Следующую передачу можно осуществлять только после выдачи предыдущего значения.

Моменты квантования по времени иногда выбираются через один и тот же интервал T₀, называемый шагом квантования по времени. Величину T₀ следует выбирать так, чтобы она не превышала длительности кода T_K. Однако более важным критерием для выбора T₀ является обеспечение адекватного отображения измеряемой величины как непрерывной функции дискретности. По известной теореме Котельникова T₀ ≤ 1 / F_СИГ, где F_СИГ – максимальная частота в спектре измеряемой величины.

Для выполнения T₀ ≥ T_K нужно по F_СИГ определить T₀, а затем T_K.

Квантование вносит определенную погрешность в процесс измерения. Общая погрешность определяется как сумма погрешностей квантования по уровню и по времени.

Погрешность квантования по уровню – методологическая погрешность, от нее нельзя избавиться.

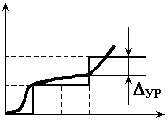
Абсолютная погрешность квантования по уровню может иметь различный знак. Для оценки погрешности квантования по уровню обычно используют понятие среднеквадратичной погрешности:

.

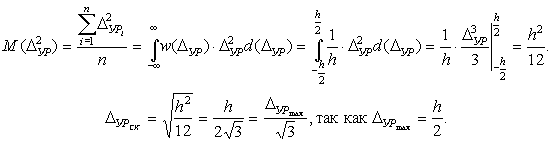
Приведенная погрешность квантования по уровню

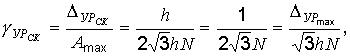
где N – количество уровней.

Если используется двоичный код, N = 2ⁿ – 1 (n – количество элементов в коде).

Можно оценить это значение уровней, или количество разрядов.

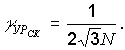
Погрешность квантования по времени необходимо знать для того, чтобы оценить те изменения измеряемой величины, которые произошли за интервал измерения T₀.

Погрешность квантования по времени является динамической погрешностью, а рассмотренная ранее погрешность квантования по уровню является статической. Для оценки выбирается среднеквадратическое значение:

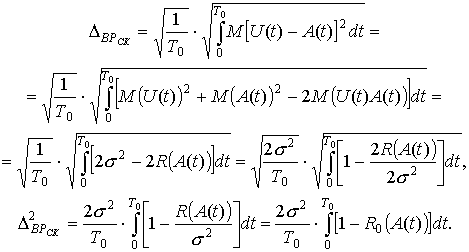
R₀(A(t)) – приведенная автокорреляционная функция. Считается, что , где постоянная корреляции.

, поэтому при разложении в ряд, откуда следует

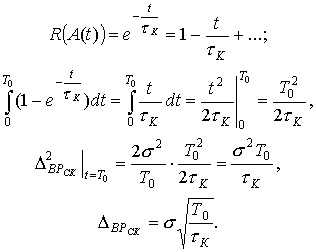
Выразив из этого уравнения T₀, можно проверить теорему Котельникова.

Зная , можно определить погрешность квантования. Суммарная среднеквадратичная погрешность передатчика

.

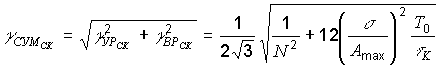Для простоты в некоторых случаях вводится другая формула. Обозначим среднюю частоту пересечения случайной величиной порога назначения. Говоря более строго, является математическим ожиданием частоты. Косвенно за скрывается подобие спектра. Если

,

что довольно часто встречается на практике, то используется теория массового обслуживания. Величина характеризует поток заявок на обслуживание информации, то есть на ее кодирование при приближении к порогу.

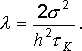
Среднюю частоту пересечения порога назначения иногда проще определить экспериментально, чем определяющие ее величины.

При разработке КС ТИ является определяющей величиной. Для различных каналов связи ориентировочно определены значения .

где N – число уровней (чем больше уровней, тем выше точность и
меньше погрешность измерения),
T₀ – шаг квантования по времени (чем больше интервал времени между опросами величины, тем больше погрешность).

Не всегда при увеличении N погрешность уменьшается, так как погрешности вносятся не только передающей стороной, но и каналом связи, а также приемной стороной.

---