Циклические коды

Циклический код – такой групповой код, все базовые комбинации которого могут быть получены из одной путем циклического сдвига ее элементов.

Циклический сдвиг кодовой комбинации – перемещение ее элементов справа налево без нарушения порядка их следования, так что крайний левый элемент занимает место крайнего правого.

В теории циклических кодов принято записывать кодовые комбинации в виде полинома некоторой фиктивной переменной x:

где aⁱ – значение символа кодовой комбинации на позиции i при нумерации справа налево;
xⁱ – 1 – фиктивная переменная в степени номера позиции i без единицы.

Пример

Представить в виде полинома кодовую комбинацию a ≈ 1011101.

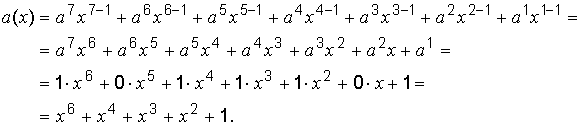
Максимальная степень x в полиноме на единицу меньше числа элементов в кодовой комбинации.

Запись комбинации в виде полинома понадобилась для того, чтобы отобразить формализованным способом операцию циклического сдвига исходной кодовой комбинации. Допустим, задана исходная кодовая комбинация и соответствующий ей полином

Умножим a(x) на x:

Так как максимальная степень x в кодовой комбинации длиной n не превышает (n – 1), то из правой части полученного выражения для получения исходного полинома необходимо вычесть aⁿ(xⁿ – 1). Вычитание aⁿ(xⁿ – 1) называется взятием остатка по модулю (xⁿ – 1). Сдвиг исходной комбинации на i тактов можно представить следующим образом: a(x)xⁱ – aⁿ(xⁿ – 1), то есть умножением a(x) на xⁱ и взятием остатка по модулю (xⁿ – 1). Взятие остатка необходимо при получении многочлена степени, большей или равной n.

Возвращаясь к определению циклического кода и учитывая запись операций циклического сдвига кодовых комбинаций, можно записать порождающую матрицу циклического кода в следующем виде:

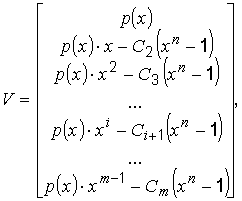
где p(x)– исходная кодовая комбинация, на базе которой получены все остальные (m – 1) базовые комбинации;

C_i = 0 или C_i = 1 (“0”, если результирующая степень полинома p(x)xⁱ не превосходит (n – 1), “1”, если превосходит).

Комбинация p(x) называется порождающей (образующей, генераторной) комбинацией. Для построения циклического кода достаточно верно выбрать p(x). Затем все остальные кодовые комбинации получаются такими же, как и в групповом коде.

Порождающий полином должен удовлетворять следующим требованиям:

1. p(x) должен быть ненулевым;
2. вес p(x) не должен быть меньше минимального кодового расстояния:
   ;
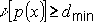3. p(x) должен иметь максимальную степень k (k – число избыточных элементов в коде);
4. p(x) должен быть делителем полинома (xⁿ – 1).

Выполнение условия 4 приводит к тому, что все рабочие кодовые комбинации циклического кода приобретают свойство делимости на p(x)без остатка. Учитывая это, можно дать другое определение циклического кода. Циклический код – код, все рабочие комбинации которого делятся на порождающую без остатка.

Свойство делимости всех комбинаций на p(x)позволяет просто записать порождающую матрицу кода в каноническом виде:

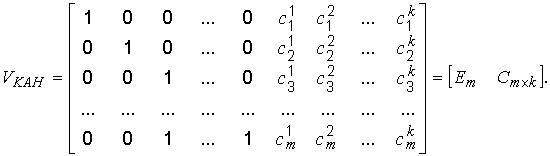
Для определения строк контрольной подматрицы поступают следующим образом:

1. любая строка единичной подматрицы записывается в виде полинома: E_i(x) = x^m-i;
2. справа к ней приписывается k нулей, что равносильно умножению на x^k: E_i(x)x^k;
3. результат делится на порождающий полином p(x):
   ;
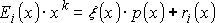   при этом остаток r_i(x) имеет степень не выше (k – 1) и содержит k элементов;
4. рабочая комбинация циклического кода состоит из m элементов единичной подматрицы и из k элементов остатка r_i(x) (он приписывается в “чистом” виде):
   

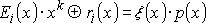
В настоящее время для облегчения процедуры построения циклических кодов их авторами найдены различные порождающие полиномы p(x) в зависимости от требований к коду. В частности, существуют таблицы с полиномами p(x) для циклических кодов с d_min= 3 (коды с d_min = 3 наиболее часто применяются на практике). Их можно найти в литературе по теории информации. Для построения кодов с d_min= 4 достаточно умножить выбранный полином p(x), найденный в таблице порождающих полиномов кодов с d_min= 3, на (x + 1), что равносильно проверке на общую четность.

Суммируя изложенное, приведем процедуру выбора p(x):

1. определить число информационных элементов m (M = 2^m) и число избыточных элементов k (если d_min= 3, 2^k = m + k + 1);
2. найти p(x) степени k по таблице (если полиномов этой степени несколько, то выбирается любой).

Разработаны циклические коды, обеспечивающие произвольное минимальное кодовое расстояние d_min ≥ 5. Они получили название БЧХ (Боуза-Чоудхури-Хоквингема, по имени разработчиков). Порождающие полиномы для таких кодов в зависимости от предъявляемых к ним требований, можно найти в табл. 5.

Табл. 5

k	n	m	s	dmin	Образующий полином
					Cимволическая запись	Запись в виде полинома
3	7	4	1	3	13	1011
4	15	11	1	3	23	10011
8	15	7	1	3	721	111010001
10	15	5	3	7	2467	10100110111
5	31	26	1	3	45	100101
10	31	21	2	5	3551	11101101001
15	31	16	3	7	107657	1000111110101111
25	31	11	5	11	5423325	101100010011011010101

Процедура построения кода БЧХ по заданным M и d_min:

1. по d_min найти значение, при котором обеспечивается необходимое число информационных элементов m при минимальной избыточности k_min;
2. найти в таблице соответствующий образующий полином;
3. если d_min четное, умножить найденный полином на (x + 1);
4. если m_ТАБЛ >> m_ЗАДАН, то можно перейти к укороченному циклическому коду, вычеркивая в порождающей матрице исходного кода с параметрами m_ТАБЛ,k_min (m_ТАБЛ – m_ЗАДАН) столбцов слева и столько же строк сверху.

---