Прием кодовых комбинаций в дискретных каналах связи с помехами

Выше были рассмотрены методы приема элементарных сигналов, которыми передавались отдельные символы кодовой комбинации. Однако сообщения в реальных системах передаются не отдельными символами, а в виде комбинаций символов (кодовых комбинаций).

Если в канале связи действует помеха, то один или несколько символов кодовой комбинации будут искажены. В результате возможны три основных случая декодирования (расшифровки) принятой кодовой комбинации:

1. правильный прием сообщения с вероятностью P_ПР (обычно P_ПР і 0,999);
2. ложный прием сообщения с вероятностью P_{Л ПР} (P_{Л ПР} Ј 10^-7), то есть ложный прием должен быть практически исключен);
3. защитный отказ, когда принимается такая кодовая комбинация, которая не может быть отождествлена ни с одним сообщением списка, то есть ни с одной разрешенной кодовой комбинацией.

В случае правильного или ложного приема система принимает сообщение, не зная о том, было ли оно искажено в канале связи. Сумма вероятностей P_ПР и P_{Л ПР} составляет вероятность приема вообще. Вероятность защитного отказа можно вычислить по формуле

P_ЗО = 1 – P_ПР – P_{Л ПР}.

Можно не рассчитывать все эти вероятности, а остановиться на двух из них. Одной из выбранных вероятностей должна обязательно быть вероятность ложного приема.

Можно говорить об еще одной вероятности: о вероятности подделки сообщения. Это случай фиксации сообщения на приемной стороне в случае, когда вообще ничего не передавалось. Подобная ситуация возникает крайне редко, поэтому эта вероятность оценивается числом сообщений за несколько лет и даже десятилетий.

Качество системы оценивается не вероятностью правильного, а вероятностью ложного приема.

Вероятности правильного, ложного приема и защитного отказа зависят как от характеристик канала связи (q, p₀, p_C), так и от количества ошибок в кодовой комбинации.

Количество ошибок принято характеризовать кратностью t. Кодовая комбинация при этом может быть искажена различным количеством ошибок во всевозможных сочетаниях от 0 до t.

В системах передачи говорят о векторе ошибки. Это число в K-ичной системе с общей значностью n (она равна значности передаваемой кодовой комбинации) и нулевыми символами на неискаженных позициях. Например, в двоичных каналах связи при передаче шестиразрядной кодовой комбинации, могут действовать такие векторы ошибки:

E₁ = 001000,

E₂ = 101000.

В первом случае искажается символ на третьей позиции, во втором – символы на первой и третьей позициях.

Для двоичного варианта вектор E определяется весом ошибки V(E). В дальнейшем будем предполагать, что используется двоичный канал связи.

Искажение передаваемой комбинации математически можно представить суммированием по модулю два неискаженной кодовой комбинации A и вектора ошибки E:

Допустим, сообщения передаются некоторыми комбинациями длиной n по симметричному каналу связи с параметрами q и p₀. Пусть на передаваемую комбинацию действует вектор ошибки E_i с весом i. Вероятность того, что кодовая комбинация будет содержать i ошибок, можно вычислить по формуле

Ошибка кратности i может произойти в

случаях, а полная вероятность появления ошибок кратности t в кодовой комбинации из n символов

Определим вероятности правильного приема, ложного приема и защитного отказа при использовании различных кодов.

1. Неизбыточный код. Для такого кода t = 0, то есть он не может не только исправить, но даже обнаружить ни одной ошибки. P_ПР = (1 – p₀)ⁿ то есть не искажен ни один из n элементов, так как код неизбыточный.
   
   (слагаемое при i = 0 составляет вероятность правильного приема). P_{З ОТ} = 0. Оценим вероятность ложного приема, принимая p₀ » 10^-4; P_{Л ПР} » n10^-4. Таким образом, неизбытточный код нельзя использовать в каналах связи с помехами, так как для него характерна большая вероятность ложного приема.
2. Избыточный код в режиме обнаружения ошибок кратности r. P_ПР = (1 – p₀)ⁿ,
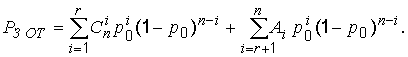
   Защитный отказ может возникать не только при ошибках кратности меньше, чем r, но и в других случаях (A_i Ј Cⁱ_n). Вероятность ложного приема
   
   B_i Ј Cⁱ_n; B_i = Cⁱ_n – A_i. Величины A_i и B_i рассчитываются экспериментально. Ввиду малой вероятности р₀ при расчете вероятности защитного отказа можно ограничиться несколькими слагаемыми: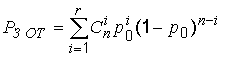
   а при определении вероятности ложного приема – только первым слагаемым.
3. Избыточный код в режиме обнаружения к ошибок и исправления s из них.
   

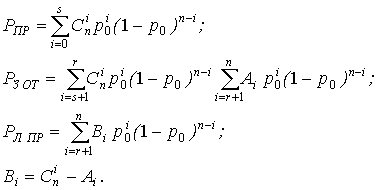
В канале связи с помехами единственным рациональным способом передачи информации является передача использование избыточных кодов, способных обнаруживать и/или исправлять ошибки.

Рассмотрим теперь подробнее способы построения таких кодов. Они были разработаны в рамках различных теорий кодирования. Наиболее развиты две ветви теоретического построения кодов: комбинаторная и алгебраическая. Комбинаторная теория кодирования основана на комбинаторике – разделе математики, изучающем свойства размещений, перестановок, сочетаний. Она начала развиваться в середине XIX века. Алгебраическая теория кодирования зародилась в конце 50-х – начале 60-х годов XX века.