Количественные характеристики помех

Важно знать не только тип помехи, но и количественные изменения, вызванные помехами. Количественные характеристики, позволяют оценить “мешающую” способность помехи, то есть степень ее влияния на передаваемый сигнал. Количественные характеристики помех представляют собой параметры, с помощью которых принято оценивать случайные процессы.

Импульсная помеха. Наиболее часто в качестве математической модели импульсной помехи выбирают закон Пуассона:

где P_(n) – вероятность появления n импульсов помехи в сигнале;
T_C – длительность информационного сигнала;
n – количество импульсов помехи, которая может исказить сигнал;
f_СП – средняя частота следования импульсов помехи.

Величина P_(n) тем меньше, чем выше кратность помехи, так как n! растет очень быстро. Как правило, все коды, обнаруживающие и/или исправляющие ошибки, строятся из расчета появления небольшого числа ошибок, так как вероятность появления ошибок большой кратности очень мала.

Отметим, что канал связи, в котором действует импульсная помеха, можно описывать по-разному. Модель Пуассона – лишь один из вариантов. Она не описывает все возможные ситуации, возникающие в таком канале связи.

Следует подробнее рассмотреть величину f_СП. Ее можно считать интенсивностью помехи только при одинаковой длительности временного интервала. В противном случае ситуация не будет отражена адекватно. Пример можно проиллюстрировать.

Если в одном канале связи средняя частота следования импульсов помехи составляет f_{СП 1} = 10 имп/с, а длительность сигнала T_{C 1} = 1 c, то величина i₁ = f_{СП 1}T _C1 = 10 имп, то есть 10 импульсов помехи исказят 10 импульсов сигнала. Допустим, в другом канале связи средняя частота следования импульсов помехи f_{СП 2} = 100 имп/с (в 10 раз больше, чем в первом канале), но длительность сигнала T_{C 2} = 0,01 c. Тогда величина i₂ = f_{СП 2} T_{C 2}= 1 имп, то есть 10 импульсов помехи исказят уже не 10, а всего 1 импульс сигнала.

Величина i = f_СПT_C в качестве количественной характеристики помехи была впервые рассмотрена Юргенсоном Р.И. Физически она представляет собой среднее число искажений в сигнале длительностью T_C.

Все системы передачи в зависимости от величины i можно разделить на три группы.

• i << 1 характерно для систем, работающих в условиях действия импульсных помех малой интенсивности.
• i = 1 – 3 имеет место в системах, работающих в условиях действия импульсных помех средней интенсивности. При этом любая передача сигнала может сопровождаться искажением. i = 3 – субъективный предел, однако говорить о большей величине нерационально, так как в подобном случае пришлось бы применять коды, исправляющие более трех ошибок. Применение же таких кодов требует неоправданных аппаратных затрат.
• i > 3 для систем, работающих в условиях помех большой интенсивности. В таких системах, возможно, действует специально организованная помеха. В рамках данного курса эти системы рассмотрены не будут.

Флуктуационная (шумовая) помеха.

Для шумовой помехи в качестве модели обычно выбирают помеху типа “белый шум”, то есть шум с неограниченным набором частот. такая модель опирается на нормальный закон распределения вероятностей. Он может быть представлен в дифференциальном и интегральном виде.

Дифференциальный вид нормального закона распределения представляет собой плотность распределения:

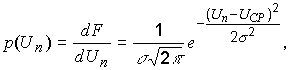
где U_n – текущее значение амплитуды шумовой помехи;

U_СР – среднее значение амплитуды шумовой помехи, это математическое ожидание

– среднеквадратическое отклонение, характеризует амплитуду переменной составляющей помехи;

D – дисперсия, вычисляемая по формуле

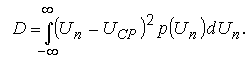
Величина (U_n – U_СР)² пропорциональна энергии, которая не зависит от знака выражения, возводимого в квадрат.

Рис.16 иллюстрирует зависимость p(U_n).

Рис. 16

Помеха малой амплитуды более вероятна, чем помеха большой амплитуды.

Интегральный вид нормального закона распределения:

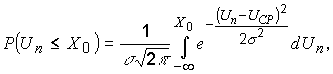
где P(U_n Ј X₀) – вероятность того, что помеха не превысит величину X₀, рис.17 показывает эту зависимость.

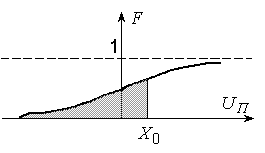
Рис. 17

Ранее было показано, что количество передаваемой информации зависит от отношения сигнал/шум. Для флуктуационной помехи эта величина может быть представлена следующим образом:

Величина тоже иногда называется отношением сигнал/шум. Если P_C / P_П і 10, то действием помехи можно пренебречь. В противном случае (что чаще всего и бывает) помеха должна учитываться в виде вероятности искажения отдельных элементарных сигналов. Помеху, однако, нельзя рассматривать как нечто фатальное. Можно изменить ситуацию. , а уровень сигнала U_СИГ зависит от проектировщика. Увеличив U_СИГ, можно увеличить (до определенных пределов). Для уменьшения вероятности появления искаженных символов можно использовать различные методы приема.

---